What is a Zero Knowledge Proof? #

Informally a zero-knowledge proof is a way to “prove” that you have access to some information without anyone else gaining access to the information itself. As you can see this is intrinsically tied to the spirit of cryptography. Most of the procedures commonly associated with cryptography are about transmitting information between two parties in such a way that the information is not able to be accessed by a non-intended (third) party. We usually handle this by employing some scheme (usually encryption) that hides the information from people who do not have access to the “keyword” which will reverse the scheme (decrypt the information). This however assumes that we can trust another party, what if we can’t? What if we have access to some sensitive information, and want to prove to someone else that we do, but do not want to give access to the information to the verifier. The most reasonable way to do this would be to have both parties communicate in a specific way (that we can formalize) such that the verifier can ask questions and the person with the information can answer them, but in a way such that it provides no new information about the object with which was discussed. This method of proving things requires interaction, and is commonly called an interactive proof system, however keep in mind that there are versions of zero-knowledge proofs that do not require interaction. The papers that introduce non-interactive zero-knowledge proofs and elaborate on them are more complicated, and require an extra assumption so we will only be talking about interactive zero-knowledge proofs, unless stated otherwise on this page.

Background Knowledge needed #

To truly gain as much as you can from this page you will need intimate familiarity with the notions of proof, probability, and at least some passing familiarity with the essence of cryptography, and set notation. While this does inherently rely on knowledge of computational complexity theory and computability theory, most of the requisites will be covered in sufficient detail. If you are still struggling, I would recommend a few textbooks or lectures on the subject, before proceeding. As with anything in mathematics, you can explore the field as deeply as you wish at any given point, and more mathematical knowledge opens up more doors with which to explore these areas.

Formalization #

Formally, an (interactive) zero-knowledge proof is a probabilistic “proof” of some statement. It is a way to verify, with an increasing level of probability, that another party has a solution to some task or access to some information that the other wishes to verify. In the theoretical papers discussing this they assume that the parties $\mathscr{A}$ and $\mathscr{B}$ are both Turing machines, which if you do not know what that means do not worry about it, just assume this means that both parties have some (finite) step-by-step procedure that they follow. So let $\mathscr{A}$ and $\mathscr{B}$ be a pair of Turing machines, such that both $\mathscr{A}$ and $\mathscr{B}$ have access to a shared sequence of sentences for input, they each have their own space which to work, they both have access to their own sequence containing random information, and there are two spaces which allow interaction. $\mathscr{A}$ has a space with which it can write to, but $\mathscr{B}$ can only read from, and $\mathscr{B}$ has a space with which it can write to, but $\mathscr{A}$ can only read from. This is called an interactive pair of Turing machines and a (self drawn) diagram of this is attached below. Treat each green arrow as the ability to write and each blue arrow as the ability to read.

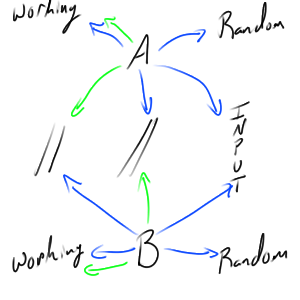
Each Turing machine takes turns on being active, and on each turn it can perform a computation, read and write to their appropriate spaces, and can send a message to the other Turing machine if it chooses. Also either Turing machine can end the process at any time that they choose. Let $\mathscr{A}$ be the prover and $\mathscr{B}$ be the verifier, such that both are working over some finite set of sentences in some language $\mathscr{L}$, with input length $n$, then if it is a zero-knowledge interactive system the following must hold:

• For any input $x \in \mathscr{L}$, $\mathscr{B}$ will accept that $\mathscr{A}$ has access to the information claimed with a probability of at least $1-\frac{1}{n^k}$, where $k$ is the number of times that $\mathscr{A}$ has passed $\mathscr{B}$’s test

• For any input $x \not\in \mathscr{L}$, $\mathscr{B}$ will accept that $\mathscr{A}$ is true with a probability of at most $\frac{1}{n^k}$

This might seem complicated but can be broken down as follows: if $x \in \mathscr{L}$ there is a way to prove to $\mathscr{B}$ that it has the information with some probability, and if $x \not\in \mathscr{L}$ then there is no way for $\mathscr{A}$ to prove to $\mathscr{B}$ that $x \in \mathscr{L}$. This is just the framework to analyze these types of problems, but doesn’t give us any way to construct these types of proofs, so lets look at a few examples.

A colorful example #

Suppose for a moment that you have a Red-Green color blind friend, $\mathscr{B}$, and you, $\mathscr{A}$, can see all colors of the visible light spectrum. You want to prove to them that you can see things that are red and green and subsequently that there actually is a distinction between these two, how can we do so? Well we could first point out random objects that are red and green in the environment and eventually $\mathscr{B}$ can memorize the objects in the environment as being red and green, but without going to another person who can see the difference between red and green, how can $\mathscr{B}$ verify the claims that $\mathscr{A}$ is making. Note that we can’t (reasonably with the technology we have), give $\mathscr{B}$ the ability to distinguish between these two, so it would make sense for $\mathscr{A}$ to create a probabilistic argument that $\mathscr{B}$ can verify independently to convince them.

So lets let $\mathscr{A}$ be our claimant, and let $\mathscr{B}$ be the verifier. Our claim that we are testing is that there is a difference between red and green. So what we do is get a pair of red and green objects that are identical except in the color. This is so that $\mathscr{B}$ can not tell the difference between the two, but note that $\mathscr{A}$ can. So we hand those two objects to $\mathscr{B}$, without telling them which object is red and which is green. Remember we only want to verify the claim, nothing more, so we do not tell $\mathscr{B}$ which object is which color, as that gives them knowledge. So $\mathscr{A}$ sits in front of $\mathscr{B}$ and hands them the two objects, one in each hand. Then $\mathscr{B}$ can turn around and conceal the objects from $\mathscr{A}$ and either switch the order of objects or keep them in the same order. $\mathscr{B}$ can then turn back around and present these two objects, and $\mathscr{A}$ should be able to verify if these objects were switched or not. Note that the size of our input is only 1 bit, so there are only two possibilities, therefore the probability of $\mathscr{A}$ guessing this correctly at random should be $\frac{1}{2^k}$, where $k$ is the number of times we have iterated through the verification process. $\mathscr{B}$ should accept the proposition with probability $1 - \frac{1}{2^k}$. After a certain number of times $\mathscr{A}$ should be able to convince $\mathscr{B}$ that they can perceive a difference between the two objects.

This is a somewhat contrived example, there is nothing that $\mathscr{A}$ loses by telling $\mathscr{B}$ the color of each object but another example will make this clear why we would desire zero information exchange.

The Cave #

Suppose that there is a shallow cave that after a while splits and becomes two paths, each of which lead to dead ends. Also suppose that $\mathscr{A}$ claims that there is a secret passage between the two forks, connecting them. $\mathscr{B}$ doesn’t believe them as they have examined both forks and see only solid stone in both paths. $\mathscr{A}$ says that they have to say a magic word in order to order to open up the passage between the two paths, but doesn’t want to show the path, or tell you the magic word as once it is revealed it will never work again. \end{minipage}

So how does $\mathscr{A}$ prove to $\mathscr{B}$ that they actually can travel between the two paths? This question requires a zero-knowledge proof to successfully answer as $\mathscr{A}$ has everything to lose if knowledge is exchanged. So what $\mathscr{A}$ should do is tell $\mathscr{B}$ to go the entrance and wait there until $\mathscr{A}$ can go down one of the paths. $\mathscr{B}$ should then go to the fork and call out to $\mathscr{A}$, and tell them which path to appear down. Note that if $\mathscr{A}$ is lying about having a secret path, the chance of $\mathscr{A}$ picking the correct path to go down at random is again $\frac{1}{2^k}$. $\mathscr{B}$ should accept the proposition that $\mathscr{A}$ is telling the truth with probability $1 - \frac{1}{2^k}$.

Now this is nice, but there is another interesting consequence of this, if some one else, lets call them $\mathscr{C}$, observed the entire proceeding, there would be no way for $\mathscr{C}$ to verify that $\mathscr{A}$ and $\mathscr{B}$ were not working together. In fact any outside observer could not verify the claims that $\mathscr{A}$ made. $\mathscr{A}$ can only convince one person at a time, and anyone watching it could not distinguish between a genuine or a false proof of the claims of $\mathscr{A}$. This is a fantastic property to have but a natural question arises, what other properties do these proofs have?

Interesting Properties #

Most of the following properties further assume that one way functions exist, which informally means that there exists a one-to-one function that is easy to perform but hard to invert. There are plenty of candidate functions that seems to fulfill this, one of which that we have touched upon in class is modular exponentiation with its inverse the discrete logarithm, another is factoring the product of two primes. However no one has proved that any proposed function actually fulfills the definition. Proving so, directly implies that $P \neq NP$ which is a famous unsolved problem in mathematics, and has a bounty of at least 1 Million US Dollars. Feel free to claim it.

One of the main, and most interesting properties is 3-colorability. Note that a graph $G$, is a set of vertices and undirected edges denoted $(V,E)$ with $E ={(v_i,v_j) \mid v_i,v_j \in V}$. If $G$ can have each one of its vertices assigned a specific integer value, such that vertices with the same integer value do not share an edge we call this a coloring of $G$. We usually only care about the minimal number of specific integers needed for a specific coloring, so if it uses at most $k$ specific integers we call this a k-coloring. Deciding if a graph has a 3-coloring is hard (in the same way that solving the discrete logarithm is), but there is a way to encode a graph in such a way that you can give a zero knowledge proof of it’s 3-colorability. You can also encode any formal mathematical proof as a graph with 3-coloring. So for every mathematical proof, there exists a zero-knowledge proof of the statement. For example, say if you proved the uniqueness of the Naiver-Stokes equations, you could encode the formal proof as a 3-coloring of some ridiculously large graph. Note that showing that there exists a 3-coloring of the graph is computationally equivalent to solving the problem from scratch, so showing the graph is not really a big deal, the 3-coloring of it is the hard part, but your mathematical proof can be encoded in that 3-coloring, and thus all you have to do to show someone that you proved the statement, without actually showing other people your proof, is setup a similar game as we did with the cave. But this time it is just on graph that we have 3-colored. They pick two vertices, and you show that the coloring for those two vertices is valid. You then recolor the graph, and they try again. If they find a vertex that has a non-valid color then they know you do not have a proof, similarly if they pick two vertices (that are connected) and they have the same color, then they also know you do not have a proof. It should also be noted that if they choose two vertices that are not connected, you don’t have to answer as it is an invalid input.

The algorithms to create this graph, and that assign the 3-coloring are reasonably quick to compute and create, however the algorithm requires too much technical knowledge to paste it here and expect everyone to understand. I would recommend looking it up in [B], especially if you have some understanding of computability and complexity theory.

From this we can encode most formal languages (not just mathematical proofs), and create zero-knowledge proofs for them, as long as they have the same type of “computational hardness” as the discrete logarithm problem.

A quick aside for Non-interactive Zero Knowledge Proofs #

I have avoided non-interactive zero-knowledge proofs as they are trickier to explain, however the practicality of these can not be understated. If we assume the existence of one way functions, and both $\mathscr{A}$ and $\mathscr{B}$ share the same source of randomness, then all we need is one communication from $\mathscr{A}$ to $\mathscr{B}$. Then we can play the same game with graph coloring. The assumptions requirements are discussed in [OW], and a discussion of how to implement a Non-interactive Zero-Knowledge proof system is discussed in [BSMP]. The algorithm to actually use this is highly non-trivial, but the knowledge of the existence non-interactive zero-knowledge proofs alone is useful.

Conclusion #

Zero-knowledge proofs are interesting objects to study in their own right, and the applications are just starting to appear. There is a significant amount of research that still needs to be done in the field as it is relatively modern in comparison to the ideas used in encryption and decryption. You could use it to send a payment over a completely insecure line, without exposing you to any attacks. Verification of private-key exchanges with arbitrary probability is trivial. Digital signing can be handled with it, without exposing either parties identity to a third party. In an increasingly connected world privacy is becoming a scarce resource, and I can only see the use of these protocols becoming more common over time.

References #

[QQQ] How to Explain Zero-Knowledge Protocols to Your Children http://pages.cs.wisc.edu/~mkowalcz/628.pdf

[B] How to Prove a Theorem So No One Else Can Claim It https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=366c58aa93307e6c20324b1a98fe199aec380fe2

[GMR] The Knowledge Complexity of Interactive Proof Systems https://people.csail.mit.edu/silvio/Selected%20Scientific%20Papers/Proof%20Systems/The_Knowledge_Complexity_Of_Interactive_Proof_Systems.pdf

[YT1] Zero Knowledge Proofs - Computerphile https://www.youtube.com/watch?v=HUs1bH85X9I

[YT2] Zero Knowledge Proof (with Avi Wigderson) - Numberphile https://www.youtube.com/watch?v=5ovdoxnfFVc

[DGOW] Honest Verifier vs Dishonest Verifier in Public Coin Zero-Knowledge Proofs https://www.math.ias.edu/~avi/PUBLICATIONS/MYPAPERS/DGOW95/dgw.pdf

[OW] One-Way Functions are Essential for Non-Trivial Zero-Knowledge https://www.math.ias.edu/~avi/PUBLICATIONS/MYPAPERS/OW93/paper.pdf

[GMW] Proofs that Yield Nothing But Their Validity or All Languages in NP Have Zero-Knowledge Proof Systems https://www.math.ias.edu/~avi/PUBLICATIONS/MYPAPERS/GMW91/GMW91.pdf

[C] The Complexity of Theorem-Proving Procedures http://www.inf.unibz.it/~calvanese/teaching/13-14-tc/material/cook-1971-NP-completeness-of-SAT.pdf

[BSMP] Noninteractive Zero Knowledge https://people.csail.mit.edu/silvio/Selected%20Scientific%20Papers/Zero%20Knowledge/Noninteractive_Zero-Knowkedge.pdf